Дискретный математический анализ (ДМА) — новый подход к анализу данных, ориентированный на исследователя и занимающий промежуточное положение между жесткими
математическими методами и мягкими нечеткими.
Важную роль в ДМА играют нечеткие множества (НМ), часть из которых является моделями дискретных аналогов фундаментальных математических свойств (близости, предельности, тренда, связности, . . .), а также нечеткая логика (НЛ), позволяющая соединить нечеткие модели в алгоритмы анализа данных, в частности, по сценариям классической математики.
В ДМА принят регрессионный подход к пределу и производной: они являются соответственно значением и угловым коэффициентом линейной регрессии, построенной по функции и нечеткой структуре на исходном конечном пространстве, моделирующей предельный переход в его точке. Таким образом, регрессионный предел и регрессионная производная существуют всегда. Возникает вопрос об их качестве, в частности, о способности увидеть дискретную гладкость. Это требует более глубокого, чем традиционный, анализа регрессии, чему и посвящена настоящая работа.

Для системы линейных алгебраических уравнений (СЛАУ) 𝐴𝑥 = 𝑏 в конечномерном
евклидовом пространстве 𝐸 с помощью ортогонализации Грама-Шмидта получено конструктивное описание многообразия ее решений Φ(𝐴, 𝑏), состоящее в ее безусловной линейной параметризации.
Это обстоятельство открывает совершенно новые возможности в использовании СЛАУ, поскольку позволяет теоретически учесть априорную информацию о свойствах истинного решения 𝑥и в его поиске на многообразии Φ(𝐴, 𝑏). Технически это выглядит так: экспертная точка зрения на решение 𝑥и формализуется неотрицательным функционалом 𝐹 на Φ(𝐴, 𝑏), а решение 𝑥и его минимизирует. Благодаря линейной параметризации Φ(𝐴, 𝑏) минимизация 𝐹 является безусловной.
Особое внимание в работе уделено случаю, когда экспертная информация о решении
𝑥и формально предстает нечеткой структурой 𝜇 весов координат пространства 𝐸, выражающих их роль в СЛАУ 𝐴𝑥 = 𝑏. Пару (𝐴𝑥 = 𝑏, 𝜇) мы называем нечеткой СЛАУ. Формирование ее решений Φ(𝐴, 𝑏, 𝜇) ⊆ Φ(𝐴, 𝑏) связано с нелинейной оптимизацией, для которой в работе разработаны алгоритмы полиномиального спуска.
Результаты исследований иллюстрируются примерами.

Многомерные гиперболо-эллиптические уравнения описывают важные физические,
астрономические и геометрические процессы. Известно, что колебания упругих мембран в пространстве можно моделировать многомерными гиперболическими уравнениями на основе принципа Гамильтона. Если предположить, что в положении изгиба мембрана находится в равновесии, то из принципа Гамильтона также следуют многомерные эллиптические уравнения.
Следовательно, колебания упругих мембран в пространстве могут быть описаны с по-
мощью многомерных гиперболо-эллиптических уравнений.
Проблема корректности задачи Дирихле для уравнений смешанного типа в специальных областях была объектом исследований многих авторов в двумерном и многомерном случаях.
Автором ранее изучена задача Дирихле для многомерных гиперболо-параболических
уравнений, показана однозначная разрешимость этой задачи, существенно зависящая от высоты рассматриваемой цилиндрической области.
В данной работе исследуется задача типа Дирихле в цилиндрической области для од-
ного класса многомерных гиперболо-эллиптических уравнений и получен явный вид её классического решения.
Показано, что однозначная разрешимость зависит только от высоты гиперболической
части цилиндрической области, а также приведён критерий единственности решения.

В работе изучается задача о представлении натурального числа 𝑛 в виде суммы квадратов четырёх простых чисел из арифметической прогрессии. Оценено, количество натуральных чисел, которые нельзя представить в указанном виде, т.е. исключительное множество задачи. Также впервые получена оценка снизу для количества представлений данного не исключительного 𝑛 в указанном виде.

Настоящая работа посвящена исследованию особенностей операторов Нийенхейса —
фундаментальных объектов нийенхейсовой геометрии. Хотя тензор Нийенхейса был введён Альбертом Нийенхейсом ещё в 1951 году, активное развитие эта область получила сравнительно недавно благодаря серии работ А.В. Болсинова, А.Ю. Коняева и В.С. Матвеева.
В размерности два известна классификация линейных операторов Нийенхейса — операторов, действующих на линейном пространстве, компоненты которых линейно зависят от координат. Существует важное взаимно однозначное соответствие между линейными операторами Нийенхейса и левосимметрическими алгебрами, что делает их классификацию эквивалентной задачей.
Несмотря на кажущуюся простоту, задача остаётся сложной даже для малых размер-
ностей и может быть решена лишь при определённых дополнительных ограничениях. В данной работе исследуются трёхмерные линейные операторы Нийенхейса (или, что то же самое, трёхмерные левосимметрические алгебры) при условии функциональной независимости коэффициентов характеристического многочлена. Полная классификация операторов с таким дополнительным условием была получена недавно, и дает список из восьми операторов.
Основной целью данной статьи является изучение особенностей таких операторов. Особой точкой называется точка, в любой окрестности которой изменяется алгебраический тип оператора (жорданова нормальная форма). В работе определены особые точки для рассматриваемого класса операторов Нийенхейса и построены их множества в трехмерном пространстве.

В работе для 𝑠⩾3 описывается алгоритм построения последовательностей 𝑃𝐻(𝑠,⃗𝑎,𝑁)𝑖 — 𝑠-мерных оптимальных коэффициентов ⃗𝑎 = (1, 𝑎, 𝑎2 (mod 𝑁), . . . , 𝑎𝑠−1 (mod 𝑁)) по модулю N, таких что 𝑎𝑠 ≡ ±1 (mod 𝑁). Строится последовательность, для ко-
торой выполнено, что погрешность численного вычисления интеграла от граничной функции класса 𝐸2 𝑠 ℎ(⃗𝑥) = 3𝑠Π︀𝑠 𝑖=1(1−2𝑥𝑖)2 по паралеллепипедальным сеткам 𝑀(⃗𝑎,𝑁) на кубе [0, 1)𝑠 убывает с ростом 𝑁.

Работа посвящена рассмотрению многокубитовых и многокудитовых квантовых систем в чистых состояниях, их описанию с точки зрения разбиения на непересекающиеся множества запутанных кубитов (кудитов) — наборы запутанности, представлена формула логарифмической запутанности многокубитовых и многокудитовых квантовых систем в чистых и смешанных состояниях. С помощью методов искусственного интеллекта произведена классификация многокубитовых систем, учитывающая максимальное по вектору состояния значение мгновенной запутанности и логарифмическую запутанность, построены диаграммы распределения этих характеристик в зависимости от факторизации вектора состояния системы на наборы запутанности. Построена формула средней по ансамблю логарифмической запутанности для многокубитовых и многокудитовых квантовых систем в
чистых состояниях.

Гельфонд получил результат о равномерной распределенности сумм цифр 𝑏-ичных разложений натуральных чисел по классам вычетов по произвольному модулю 𝑑. Позднее Ламбергер и Тусвальднер, используя глубокие оценки тригонометрических сумм, получили налог теоремы Гельфонда, в котором вместо 𝑏-ичных разложений используются разложения по линейным рекуррентным последовательностям, удовлетворяющим условию Парри и некоторому дополнительному условию на коэффициенты. В статье мы даем новое, более простое и самозамкнутое доказательство теоремы Ламбергера – Тусвальднера.
Наше доказательство носит чисто комбинаторный характер и требует только условия Парри. Кроме того, мы даем достаточно простую явную формулу для показателя степени в остаточном члене. В отличие от результата Ламбергера – Тусвальднера, полученный нами показатель зависит только от 𝑑 и порядка линейной рекуррентной последовательности, но не от ее коэффициентов. Однако наш результат не включает равнораспределенность по модулю 𝑑 сумм цифр натуральных чисел, пробегающих арифметические прогрессии, что также было доказано Ламбергером и Тусвальднером.
В конце работы кратко обсуждаются некоторые нерешенные задачи.

Проблема проверки полноты конечных подмножеств играет важную роль при исследовании функциональных систем. В классе конечных автоматов с операциями композиции задача проверки полноты конечных подмножеств является алгоритмически неразрешимой, тогда как класс конечных автоматов с операциями суперпозиции не содержит конечных полных систем. Подкласс дефинитных автоматов характеризуется наличием конечных полных систем относительно операций суперпозиции, однако задача проверки полноты конечных подмножеств в данном случае также оказывается алгоритмически неразрешимой. Ранее был рассмотрен класс линейных автоматов с операциями композиции.
Для данного класса был получен алгоритм определения полноты конечных подмножеств.
В то же время для линейных автоматов с операциями суперпозиции было установлено отсутствие конечных полных систем. Интерес представляет рассмотрение данной задачи применительно к классу дефинитных линейных автоматов с операциями суперпозиции. В данной работе был получен алгоритм проверки полноты конечных содержащих константу ноль подмножеств в классе дефинитных линейных автоматов.

Для количества нулей дзета-функции Римана 𝜁(𝑠) в узких прямоугольниках критической полосы (Re 𝑠 ⩾ 𝛼 ⩾ 0,5 и 𝑇 < Im𝑠 ⩽ 𝑇 + 𝐻), при

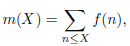
где (𝜅, 𝜆) — произвольная экспоненциальная пара, 𝜀 < 10^(−4) — любое фиксированное положительное число, 𝑇 ⩾ 𝑇0(𝜀) > 0, получена оценка вида

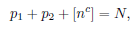
причём 𝑎 = 2, 4, 𝑐 = 172, если 1/2 ⩽ 𝛼 ⩽ 2/3 или 5/6 ⩽ 𝛼 ⩽ 1, и соответственно 𝑎 = 8
3 , 𝑐 = 50, если 2/3 < 𝛼 < 5/6 .

При 𝐻 ⩾ 𝑁^(1− 1/2𝑐 ) (ln𝑁)^2, где L = ln𝑁, а 𝑐 — нецелое фиксированное число, удовлетворяющее условиям 

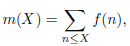
получена асимптотическая формула для количества представлений достаточно большого
натурального числа 𝑁 в виде

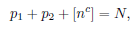
где 𝑝1, 𝑝2 — простые числа, 𝑛 — натуральное число,

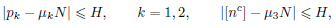
𝜇1, 𝜇2, 𝜇3 — положительные фиксированные числа, причём 𝜇1 + 𝜇2 + 𝜇3 = 1.

В статье на классе K бесконечных двоичных последовательностей без 1-серий строит-
ся согласованное распределение вероятностей P, которое индуцируется однородной цепью Маркова с матрицей перехода за один шаг P𝜑 , и полностью определяемой золотым сечением 𝜑. Использование цепи Маркова при построении вероятностной меры P позволяет применить теорему А.Н. Колмогорова о продолжении меры. Асимптотическое распределение подкласса K 0 бесконечных двоичных последовательностей без 1-серий, начинающихся с нуля, совпадает с аналогичным асимптотическим распределением классической равновероятностной модели. При этом асимптотическое распределение данного класса K^0 совпадает с вероятностью P(K^0).

В статье рассматривается задача нахождения количества натуральных чисел, не превосходящих наперед заданного 𝑛, удовлетворяющих некоторым условиям на функцию 𝜈(𝑚) – количество простых делителей числа 𝑚. Данная работа обобщает результат М. В. Левека, который рассматривал значения функции 𝜈 в соседних точках натурального ряда. В статье же значения данной функции рассматриваются в соседних точках арифметической прогрессии. Решение опирается на взаимную простоту и следующую из этого «статистическую независимость» простых делителей соседних членов арифметической прогрессии.

Работа посвящена изучению интегрирования уравнения Гарри Дима с самосогласо-
ванным источником. Источник состоит из комбинации собственных функций и линейно-независимого решения с теми же собственными функциями соответствующей спектральной задачи для уравнения струны, не имеющего спектральных особенностей. При рассмотрении источника точки дискретного спектра уравнения струны есть функции от времени.
Выведены временные характеристики данных рассеяния уравнения струны, которые позволяют интегрировать задачу Коши для уравнения Гарри Дима со специальным самосогласованным источником в классе быстроубывающих функций методом обратной задачи рассеяния.

В статье показано, что между действиями симметрической группы 𝑆𝑛 подстановок
на множестве линейных диофантовых уравнений и на множестве их решений существует прямая связь.
Так, удалось установить, что при перестановке коэффициентов линейного диофантова
уравнения координаты его вектора общего решения переставляются в том же порядке, а при перестановке переменных — в обратном порядке.
Аналогичная связь имеется и между действиями группы автоморфизмов целых чисел
на множестве линейных диофантовых уравнений и их решений: если какие-либо коэффициенты в уравнении заменить на им противоположные, то соответствующие по порядку следования координаты его вектора общего решения также заменятся на им противоположные.
Были также получены результаты, которые касаются связи разных действий группы
подстановок на множестве линейных диофантовых уравнений. Например, перестановка коэффициентов уравнения означает перестановку его неизвестных в обратном порядке.
Установленные связи между действиями позволяют на практике быстрее находить ре-
шения целого класса линейных диофантовых уравнений, зная решение всего одного его представителя. В свою очередь, изучение действий других групп на данном множестве и связей, порожденных ими, позволит расширить этот класс.

Представлены двухконстантные формы связей между напряжениями и деформациями
нелинейно-упругих изотропных материалов. Такого рода материалы могут использоваться для гашения колебаний строительных конструкций при динамических воздействиях (землетрясения, ударные волны при взрывах). Свободная энергия рассматриваемых соотношений представляется функцией алгебраических инвариантов тензора деформаций Коши-Грина либо естественных инвариантов «левого» тензора деформаций Генки. Разработана методика определения констант представленных связей между напряжениями и деформациями. Предлагаемая методика основана на анализе экспериментальных зависимостей окружных деформаций на внешней и внутренней поверхностях от приложенного
внутреннего давления и решениях задачи Ламе для полого цилиндра в плоском деформированном состоянии. Показано, что конкретизация приведенных определяющих соотношений возможна на основе выделения линейного участка экспериментальных зависимостеи построения теоретических зависимостей в предположении малости деформаций. Таким образом, следующие за линейным участком данные могут быть использованы для конкретизации модулей упругости третьего порядка определяющих соотношений, построенных на основе рассмотренных. Следовательно, изложенную в работе методику можно также
рассматривать как частичное решение задачи конкретизации связей между напряжениями и деформациями, включающих модули упругости третьего порядка. Для представленных экспериментальных данных показано, что результаты конкретизации по выдвинутой методике соответствуют определенным с помощью классического эксперимента на растяжение модулям упругости. Приведенная методика может использоваться как непосредственно, так и с целью минимизации числа экспериментов в задачах конкретизации определяющих значений нелинейной теории упругости.

В статье рассматривается задача о дифракции цилиндрической гармонической звуко-
вой волны на неоднородном жидком сфероиде с абсолютно жестким шаровым включением. Полагается, что квадрат эксцентриситета сфероида является малой величиной. Сфероид помещен в безграничную однородную сжимаемую идеальную жидкость. Линейный источник, генерирующий звуковые волны, параллелен оси вращения сфероида. Материал сфероида характеризуется переменными плотностью и скоростью звука, которые являются непрерывными функциями радиальной координаты.
Методом возмущений получено приближенное аналитическое решение задачи с использованием разложений по волновым сферическим функциям.
Представлены результаты численных расчетов диаграмм направленности рассеянного
акустического поля в дальней зоне.

В работе в модельной ситуации исследуется обобщенное решение задачи Коши линеаризованного уравнения Кортевега – де Фриза. Решение представляется в виде тригонометрического ряда Виноградова, что позволяет свести вывод к методу Виноградова тригонометрических сумм Г. Вейля.

Настоящая работа посвящена изучения свойств специальной построенной функции
𝜙𝜎(𝑦, 𝑥), которая задана в бесконечной области D трехмерного евклидова пространства.
В данной работе доказываются результаты, позволяющие утверждать ограниченность бигармонической функции внутри некоторой трехмерной области, если она ограничена со своей нормальной производной на границе этой области.

Исследуется задача нахождения стационарной цепи Маркова с максимальной энтропией на множестве бесконечных двоичных последовательностей, запрещающих появление трёх единиц подряд. Установлена связь этой задачи с системой счисления с нецелым основанием, изученной А. О. Гельфондом. Дана вероятностная интерпретация распределения остатков Гельфонда в терминах эргодической цепи Маркова с тремя состояниями. В качестве основного результата явно указаны параметры искомой экстремальной цепи. Показано, что матрица переходных вероятностей и стационарное распределение выражаются через корень 𝜃 > 1 уравнения 1 = 𝜃−1 + 𝜃−2 + 𝜃−3. Энтропия найденной цепи равна ln 𝜃, что определяет максимально достижимую непредсказуемость в классе рассматриваемых
последовательностей с данным запретом.

Линейное пространство операторных полей, состоящее из операторов Нийенхейса, на-
зывают пучком Нийенхейса. Интересными примерами таких пучков являются максимальные (по включению) пучки Нийенхейса. Случай, когда максимальный пучок Нийенхейса содержит подпучок симметричных постоянных (𝑛 × 𝑛)-матриц (в некоторой фиксированной системе координат), недавно рассматривался в работе [4], в которой было получено полное описание таких максимальных пучков при 𝑛 ⩾ 3. Как оказалось, случай 𝑛 = 2 требует отдельного исследования. Эта задача решена в данной работе.